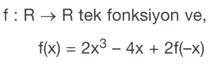Fonksiyonların Dönüşümleri - 1
Bol Bol test çöz ve kendini daima sınava hazır tut.Fonksiyonların Dönüşümleri - 1
11. Sınıf: Matematik. Fonksiyonlarda Uygulamalar. Fonksiyonların Dönüşümleri. Test Soruları
Hatırlatma!
TestSorular'da sadece oturum açmış öğrenciler çözdükleri testlerden puan kazanabilir.
Yok benim amacım puan toplamak değil sadece kendimi geliştirmek istiyorum diyorsan, sorular seni bekliyor.
Hata Bildir!
y = f(x) fonksiyonunun grafiği üzerinde bir nokta (-3, 3) tür.
(0, - 2) noktası y = -f(x + 3) + 1 fonksiyonunun grafiği üzerindedir.
Yapılan işlemle y = f(x) fonksiyonunun grafiğinden y = f(x + 3) fonksiyonunun grafiği elde ediliyor.
y = f(x) fonksiyonunun grafiği x ekseninde 3 birim sola öteleniyor.
f, R'den R'ye tanımlı çift fonksiyon olmak üzere,
f(4) = m + 7
f(-4) = 5 - m
y = f(x) fonksiyonunun grafiği y ekseninde 4 birim aşağı öteleniyor.
f(x) çift, g(x) tek fonksiyon olmak üzere,
f(2) = 3
g(-3) = - 2
şeklindedir.
f( - x) - f(x) = 0 dır.
3f(-x) + 4f(x) = 7x2 + 7
şeklindedir.
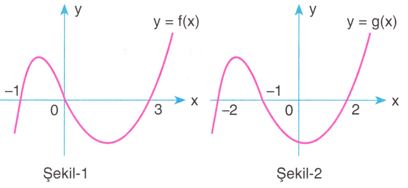
Koordinat düzleminde y = f(x) fonksiyonunun grafiği veriliyor. f(x) fonksiyonunun grafiğinin
I. x eksenine göre simetriği alınırsa y = —f(x)
II. y eksenine göre simetriği alınırsa y = f(-x)
III. Orijine göre simetriği alınırsa y = -f(-x ) fonksiyonunun grafiği elde edilir.
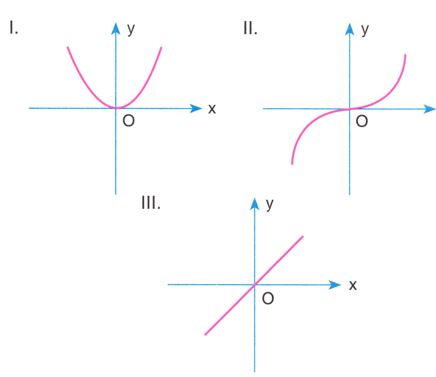
I. f(-x) = f(x) koşulunu sağlayan f(x) fonksiyonuna çift fonksiyon denir.
II. f(-x) = -f(x) koşulunu sağlayan f(x) fonksiyonuna tek fonksiyon denir.
III. Çift fonksiyon grafikleri y eksenine, tek fonksiyon grafikleri orijine göre simetriktir.
f, R'den R'ye tanımlı tek fonksiyon olmak üzere,
f(3) = m - 8
f(-3) = m + 6
f, R'den R'ye tanımlı tek fonksiyon olmak üzere,
f(2) + f(3) = 6
şeklinde verilmiştir.
y = f(x) fonksiyonunun grafiği önce 3 birim sola sonra 4 birim aşağı öteleniyor.
f(x) = 1x1 + 1
Koordinat düzleminde y = f(x) fonksiyonunun grafiği veriliyor.