İkinci Dereceden Fonksiyonlar ve Grafikleri - 2

a gerçek sayı olmak üzere,
y = - x2 - 2(a - 1)x + 3

parabolünün tepe noktasının geometrik yerinin denklemi aşağıdakilerden hangisidir?

y = 3 - x2 E) y = 5x - y = x2 + 3 y = 3x + y = 1 - x2

Yukarıda verilen y = f(x) parabolünün denklemi aşağıdakilerden hangisidir?

y = - x 2+ x + 2 y = - x 2+ 2 x + 3 y = x2 - x - 2 y = - x 2 - x + y = - 2 x 2+ x + 4

Aşağıdaki şekilde grafiği verilen
y = ax2 + (1 + a)x + 1 parabolünün tepe noktası T
noktasıdır. T noktası y ekseni üzerinde, A noktası da
x ekseni üzerindedir.

[TO] ı [OA] olduğuna göre, a kaçtır?

-2 2 1 -1 0

f : R -> R olmak üzere,
f(x) = 3x2 - mx + n
fonksiyonunun simetri ekseni parabolü (-2, m) noktasında kesmektedir.

Buna göre, m.n çarpımı kaçtır?

12 24 -12 -3 0

f(x) = 2.(x + 1 ).(x + 3) - 3x.(x - 2)

parabolünün tepe noktasının koordinatları toplamı kaçtır?

60 62 55 55 57

y = x2 - (m + 2)x + 2m - 1
parabolünün tepe noktası Oy ekseni üzerindedir.

Buna göre, fonksiyonun y eksenini kestiği noktanın ordinatı kaçtır?

-3 -5 1 0 -2

Şekilde verilen y = f(x) bir paraboldür.

Buna göre, f(2) kaçtır?

-6 4 -4 -1 2

Yukarıdaki şekilde gerçek sayılarda tanımlı,
f(x) = x2 - mx + 3m
fonksiyonunun grafiği verilmiştir.

IABI = 2IOAI olduğuna göre, m aşağıdakilerden hangisidir?

15 12 16 9 6

Yukarıdaki şekilde,
y = - x2 - 4x + n
fonksiyonunun grafiği verilmiştir.

Bura göre, n kaçtır?

-2 1 -1 0 2

Şekildeki grafik aşağıdaki fonksiyonlardan hangisine aittir?

y = 2(x - 1 )2 y = (x + 1 ) y = 2(x + 1) y = x2 - 2x y = x2 - 4

Tepe noktası T (- 2, 1) olan ve A (- 1, 2) noktasından geçen parabolün denklemi aşağıdakilerden hangisidir?

y = (x + 2)2 + 1 = (x - 2)2 + 1 y = 2(x + 2)2 + 1 y = - ( x + 2)2 + 1 y = -(x + 2)2 + 2

A(1, 2) , B(- 1, 2) , C(0, - 3 )
noktalarından geçen parabolün denklemi,
y = ax2 + bx + c

olduğuna göre, a - b . c kaçtır?

0 -3 6 5 8

t reel sayı olmak üzere,

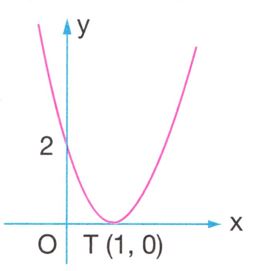
A(t - 1, 2t2 + 1) noktalarının analitik düzlemde çizdiği eğrinin denklemi aşağıdakilerden hangisidir?

y = - 2(x + 1)2 + 1 y = 2x2 + 4x + 3 y = 2(x + 1) y = - 2x2 + 1 y = - 2x2 - 4x + 3

Tepe noktası T(- 1, 1) olan parabol orijinden geçmektedir.

Buna göre, parabolün denklemi aşağıdakilerden hangisidir?

y = x2 + 2x y = x2 - 2x y = - ( x + 1 )2 — 1 y = (x + 1)2 + y = - x2 - 2x

y = x2 + (m - 4)x + 9 parabolünün simetri ekseni x = 6 doğrusudur.

Buna göre, m kaçtır?

-2 -8 -4 -6 -10

y = x2 + (m - 2)x - 2m
parabolünün tepe noktası T(r, 0) şeklindedir.

Buna göre, m kaçtır?

-2 -3 -4 -5 0

A(0, 3), B (- 1, 2) ve C(1, 6) noktalarından geçen parabolün denklemi aşağıdakilerden hangisidir?

y = 2x2 - 3x + 3 y = 3 - 2x - x2 y = 3 - x2 y = x2 + 2x + 3 y = x2 - 2x + 3

m e R olmak üzere,
y = x2 - 2mx + 3

parabollerinin tepe noktalarının geometrik yerinin denklemi aşağıdakilerden hangisidir?

y = 3 - x2 y = 1 - x2 y = x2 + y = 2 - x2 y = x2 +

Şekilde y = f(x) = x2 - 6x + 5 fonksiyonunun grafiği verilmiştir.

Buna göre, a + b + c toplamı kaçtır?

9 8 6 11 4

Şekilde, y = x2 + 3x - 5 parabolü gösterilmiştir.

Buna göre, A.B.C çarpımı kaçtır?

25 18 20 15 -25

Son

Üye Ol Puan Kazan!

Sitemize üye olup çözdüğünüz testlerden puanlar kazanarak çok yakında hizmete girecek olan e-Mağaza uygulamamızda sunulan hediyelere ücretsiz sahip olabilirsiniz.

Sitemize üye olmak ve e-Mağaza uygulamasındaki kitablarımız tamamen ücretsizdir.

Oturum Aç Kayıt Ol

İkinci Dereceden Fonksiyonlar ve Grafikleri - 2

İkinci Dereceden Fonksiyonlar ve Grafikleri - 2

Hatırlatma!

Son

Üye Ol Puan Kazan!

Başka Soru Kalmadı

Soru Listesi