Noktanın Analitiği - 3
Bol Bol test çöz ve kendini daima sınava hazır tut.Noktanın Analitiği - 3
11. Sınıf : Matematik - Analitik Geometri - Noktanın Analitiği Test Soruları
Hatırlatma!
TestSorular'da sadece oturum açmış öğrenciler çözdükleri testlerden puan kazanabilir.
Yok benim amacım puan toplamak değil sadece kendimi geliştirmek istiyorum diyorsan, sorular seni bekliyor.
Hata Bildir!
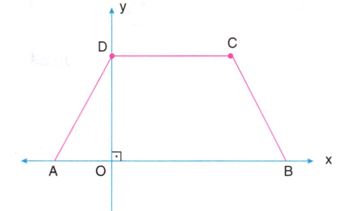
Aşağıdaki şekilde verilen ABCD bir konkav dörtgen ve köşeleri A (-4 , 0), B(6, 0), C(1, 1), D(6, 6) noktalarıdır.
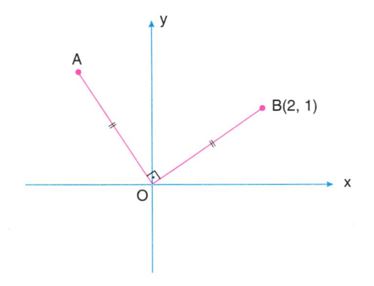
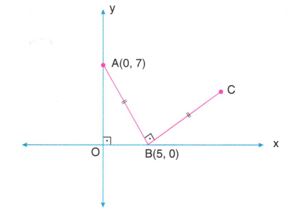
Aşağıdaki şekilde |AB| = |BC|, |DE| = 2.|CD| ve E(8, -3) olmak üzere,
• B noktasının apsisi -6
• D noktasının ordinatı -5
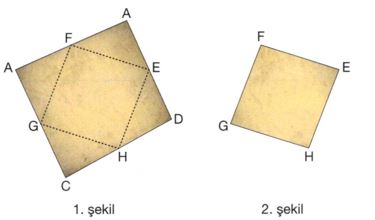
1. şekilde görülen, ABCD dörtgeni biçimindeki kâğıt, bulundukları kenarların orta noktaları gösteren E, F, G ve H noktalarını birleştiren kesikli çizgiler boyunca kesilip,
2. şekildeki gibi EFGH dörtgeni biçimindeki kısmı alınarak diğer dört küçük parçası atılmıştır. Son görünüm analitik düzleme aktarıldığında; E(a, 10), F(b, c), G(-12, -6) ve H(4,0) koordinatlarıyla köşe noktaları temsil edilirken, kâğıdın köşegenleri de y ekseni üzerinde kesişmektedir.
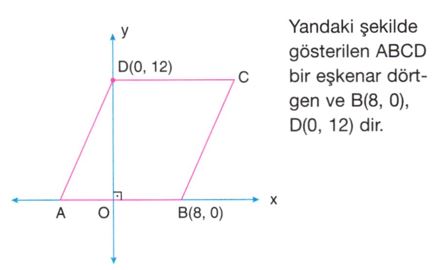
Şekilde görülen ABCD dörtgeni biçimindeki karton parçası BD köşegeni boyunca katlandığında A köşesi C köşesi üzerine gelmiş, sonra tekrar geri açılmıştır.
Karton analitik düzlemin I. bölgesinde modellendiğinde; D köşesi orijinde, AD ve DC kenarları sırasıyla ordinat ve apsis ekseni üzerinde, B ve C köşeleri sırasıyla
(a, 4) ve (2, 0) koordinatlarında bulunmaktadır.

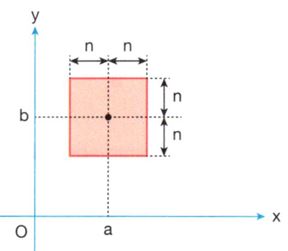
Koordinat sisteminde alınan bir A(a, b) noktasından n birim aşağıda, n birim yukarıda, n birim sağda ve n birim solda bulunan doğruların kesişim bölgesinde
yer alan kare A(a, b)n ile gösteriliyor.
a > 0 ve b > 0 olmak üzere, A(a, b)n ifadesinin belirttiği kare aşağıdaki şekilde gösterilmiştir.
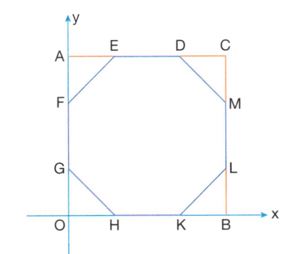
Şekilde, analitik düzlemdeki AOBC dörtgeni üzerinde kenarları bulunan, DEFGHKLM düzgün sekizgeni görülmekte olup, sekizgenin çevresi 16 birimdir.
Buna göre;
I. D (2 + V2, 2V2 + 2) dir.
II. Düzgün sekizgenin simetri merkezinin x ve y koordinatlarına uzaklıklarının toplamı 2 + 2V2 birimdir.
III. Alan(AOBC) = 8 + 4>/2 birim karedir.
Koordinat sisteminde
A(1, 4), B(-2, 2), C(0, 8), D(-6, k)
noktaları veriliyor.
Analitik düzlemde A ( - 1,10) olmak üzere, ABC üçgeninin ağırlık merkezinin koordinatları G(1, 2) dir.